참고)
https://velog.io/@gimtommang11/%EC%9E%90%EB%A3%8C%EA%B5%AC%EC%A1%B0%EA%B7%B8%EB%9E%98%ED%94%84
https://gmlwjd9405.github.io/2018/08/13/data-structure-graph.html
https://velog.io/@pa324/%EC%9E%90%EB%A3%8C%EA%B5%AC%EC%A1%B0-%EA%B7%B8%EB%9E%98%ED%94%84-n8k1e9v4jo
그래프(Graph)
- 정점(node)과 정점을 연결하는 간선(edge)의 연결을 시각적으로 표현한 자료구조 입니다.
- 그래프의 종류에는 무방향 그래프, 방향 그래프, 가중치 그래프 등이 있습니다.
- 구현 방법으로는 인접행렬(2차원배열), 인접리스트(리스트)이 있습니다.
- 부모, 자식 관계가 없습니다.
그래프 용어
- 정점(vertex) : 그래프를 형성하는 노드(원을 이용해 위치를 표현합니다.)
- 간선(edge) : 그래프에서 정점(node) 간의 연결, 즉 정점(node)을 연결하는 선을 의미합니다.
- 정점 차수 : 해당 정점(node)에 연결된 총 간선의 개수를 의미합니다.
- 인접 정점 : 해당 정점과 간선에 의해 연결된 정점
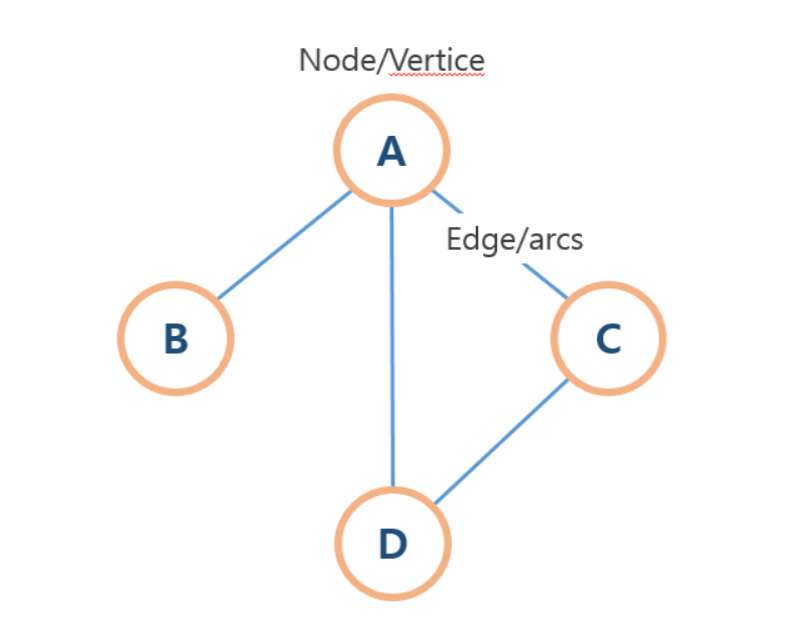
용어 설명
정점 : A, B, C, D
간선 : 정점과 정점 사이에 연결된 모든 파란색 선
정점 차수 : A : 3개, B : 1개, C : 2개, D : 2개
인접 정점
{A : B, C, D}
{B : A}
{C : A, D}
{D : A, C}
무방향 그래프(Undirected Graph)
- 두 정점이 각각 간선으로 연결되어 있고 간선의 방향이 없는 그래프(두 정점 모두 간선을 통해 양 방향을 이동 가능)
- 정점 A와 정점 B를 연결하는 간선 (A, B), (B, A) 모두 동일합니다
- ex) 양방향 통행 도로
- 표현하는 방식으로는 인접 행렬, 인접 리스트가 있습니다.
무방향 가중치 그래프 구현
code
// ---------------- Graph 클래스 생성 ----------------
function undirectedGraph() {
this.edges = {};
}
// ---------------- 간선, 정점 추가 ----------------
undirectedGraph.prototype.addVertex = function(vertex) {
this.edges[vertex] = {};
}
undirectedGraph.prototype.addEdge = function(vertex1, vertex2, weight) {
if(weight == undefined) {
weight = 0;
}
this.edges[vertex1][vertex2] = weight;
this.edges[vertex2][vertex1] = weight;
}
// ---------------- 간선, 정점 삭제 ----------------
undirectedGraph.prototype.removeEdge = function(vertex1, vertex2) {
if(this.edges[vertex1] && this.edges[vertex1][vertex2] != undefined) {
delete this.edges[vertex1][vertex2]
}
if(this.edges[vertex2] && this.edges[vertex2][vertex1] != undefined) {
delete this.edges[vertex2][vertex1]
}
}
undirectedGraph.prototype.removeVertex = function(vertex) {
for(var removeVertex in this.edges[vertex]) {
this.removeEdge(removeVertex, vertex);
}
delete this.edges[vertex]
}
// ---------------- 예제 ----------------
var graph1 = new undirectedGraph();
// 정점 추가
graph1.addVertex(1);
graph1.addVertex(2);
graph1.addVertex(3);
graph1.addVertex(4);
console.log(graph1)
// undirectedGraph { edges: { '1': {}, '2': {}, '3': {}, '4': {} } }
// 간선 추가
graph1.addEdge(1, 2, 1)
graph1.addEdge(2, 3, 10)
graph1.addEdge(3, 1, 15)
graph1.addEdge(4, 1, 5)
console.log(graph1)
// undirectedGraph {
// edges: {
// '1': { '2': 1, '3': 15, '4': 5 },
// '2': { '1': 1, '3': 10 },
// '3': { '1': 15, '2': 10 },
// '4': { '1': 5 }
// }
// }
// 정점, 간선 삭제
graph1.removeVertex(2)
graph1.removeEdge(1, 3)
console.log(graph1)
// undirectedGraph {
// edges: { '1': { '4': 5 }, '3': {}, '4': { '1': 5 } }
// }
설명
// ---------------- Graph 클래스 생성 ----------------
function undirectedGraph() {
this.edges = {};
}
// ---------------- 간선, 정점 추가 ----------------
// 정점 추가
undirectedGraph.prototype.addVertex = function(vertex) {
this.edges[vertex] = {};
}
// 두 정점 간의 간선 추가
undirectedGraph.prototype.addEdge = function(vertex1, vertex2, weight) {
if(weight == undefined) {
weight = 0;
}
// vertex1 정점, vertex2 정점 모두 가중치가 있는 간선을 추가하는 코드
this.edges[vertex1][vertex2] = weight;
this.edges[vertex2][vertex1] = weight;
}
// ---------------- 간선, 정점 삭제 ----------------
// 두 정점 간의 간선 삭제
undirectedGraph.prototype.removeEdge = function(vertex1, vertex2) {
// (vertex1 간선의 존재 여부) && (vertex1과 vertex2가 간선으로 연결되어 있는지 여부) 참이면
// vertex1정점에 연결되어 있는 vertex2정점 과의 간선을 삭제
if(this.edges[vertex1] && this.edges[vertex1][vertex2] != undefined) {
delete this.edges[vertex1][vertex2]
}
// (vertex2 간선의 존재 여부) && (vertex2와 vertex1이 간선으로 연결되어 있는지 여부) 참이면
// vertex2정점에 연결되어 있는 vertex1정점 과의 간선을 삭제
if(this.edges[vertex2] && this.edges[vertex2][vertex1] != undefined) {
delete this.edges[vertex2][vertex1]
}
}
// 해당 정점 삭제
// 1. 해당 정점에 연결되어 있는 모든 간선을 삭제한다.
// 2. 해당 정점을 삭제한다.
undirectedGraph.prototype.removeVertex = function(vertex) {
// 해당 정점의 연결되어 있는 모든 간선을 반복문을 통해 삭제하는 코드
for(var removeVertex in this.edges[vertex]) {
this.removeEdge(removeVertex, vertex);
}
// 해당 정점 삭제
delete this.edges[vertex]
}
// ---------------- 예제 ----------------
var graph1 = new undirectedGraph();
// 정점 추가
graph1.addVertex(1);
graph1.addVertex(2);
graph1.addVertex(3);
graph1.addVertex(4);
console.log(graph1)
// undirectedGraph { edges: { '1': {}, '2': {}, '3': {}, '4': {} } }
// 간선 추가
graph1.addEdge(1, 2, 1)
graph1.addEdge(2, 3, 10)
graph1.addEdge(3, 1, 15)
graph1.addEdge(4, 1, 5)
console.log(graph1)
// undirectedGraph {
// edges: {
// '1': { '2': 1, '3': 15, '4': 5 },
// '2': { '1': 1, '3': 10 },
// '3': { '1': 15, '2': 10 },
// '4': { '1': 5 }
// }
// }
// 정점, 간선 삭제
graph1.removeVertex(2)
graph1.removeEdge(1, 3)
console.log(graph1)
// undirectedGraph {
// edges: { '1': { '4': 5 }, '3': {}, '4': { '1': 5 } }
// }
방향 그래프(Directed Graph)
- 두 정점이 간선으로 연결되어 있고 한 정점에만 간선의 방향이 있는 그래프(간선의 방향이 있는곳만 이동할수 있다)
- 정점 A와 정점 B를 연결하는 A -> B 간선이 있다면 (A, B)로만 이동 가능하고 (B, A)로는 이동 불가능
- ex) 일방 통행
- 표현하는 방식으로는 인접 행렬, 인접 리스트가 있습니다.
방향 가중치 그래프 구현
code
function directedGraph() {
this.edges = {};
}
directedGraph.prototype.addVertex = function(vertex) {
this.edges[vertex] = {}
}
directedGraph.prototype.addEdge = function(goVertex, stopVertex, weight) {
if(weight == undefined) {
weight = 0
}
this.edges[goVertex][stopVertex] = weight;
}
directedGraph.prototype.removeEdge = function(goVertex, stopVertex) {
if(this.edges[goVertex] && this.edges[goVertex][stopVertex] != undefined) {
delete this.edges[goVertex][stopVertex];
}
}
directedGraph.prototype.removeVertex = function(vertex) {
for(var allEdge in this.edges[vertex]) {
this.removeEdge(allEdge, vertex);
}
delete this.edges[vertex]
}
var graph2 = new directedGraph();
graph2.addVertex('A')
graph2.addVertex('B')
graph2.addVertex('C')
graph2.addEdge('A', 'B', 1)
graph2.addEdge('B', 'C', 1)
graph2.addEdge('C', 'A', 1)
console.log(graph2.edges)
// { A: { B: 1 }, B: { C: 1 }, C: { A: 1 } }
graph2.removeEdge('A', 'B')
graph2.removeVertex('B')
console.log(graph2.edges)
// { A: {}, C: { A: 1 } }
'자료구조' 카테고리의 다른 글
| 힙 정렬(Heap Sort) (0) | 2020.07.10 |
|---|---|
| 큐(Queue) 스택(Stack) (0) | 2020.07.09 |
| 해시 테이블(Hash Table) (0) | 2020.07.08 |
| 병합 정렬(Merge Sort) (0) | 2020.07.07 |
| 빠른 정렬(Quick Sort) (0) | 2020.07.03 |